参考文献 1 では, 高木貞治氏の書いた解析概論の緒言として示されている三角関数の古典的な導入法の問題点と,
それに対する合理的な導入, 定義に関する記述があり, 興味深かったので読んでいたのだが,
ふと高校数学 Ⅲ の「普通な」加法定理や積和, 和積の公式, 導関数の導出などが頭から抜けていたので, 復習がてら書くことにした.
一応, このエントリで言う三角関数 \(\cos\theta,\sin\theta\) の定義は高校数学の範囲で言われる定義と同様であり, 次のとおりである.
直行座標平面上の原点 \(O\left(0,0\right)\) を中心とする半径 \(1\) の円 \(C\) の \(x\geq 0,y\geq 0\) の部分を \(C_{+}\) としたとき,
弧度法によると, 点 \(A\left(1,0\right)\), \(C_{+}\) 上の点 \(P\left(x,y\right)\) を角 \(A O P\) が \(\theta\ \left(0\lt\theta\leq\frac{\pi}{2}\right)\) となるようにとれば,
孤 \(A P\) の長さは 角 \(A O P\) そのもの, すなわち \(\theta\) である. このとき \(x=\cos\theta,y=\sin\theta\) である.
よくよく考えてみれば, この定義では,
孤 \(A P\) の長さおよび実数 \(0\lt\theta\leq\frac{\pi}{2}\) に対し孤 \(A P\) の長さが \(\theta\) となる \(C_{+}\) 上の点
\(P\) が存在することについて, 特に説明しておらず, 定義としては不十分な点があることが考えられる.
参考文献 1 にはこの問題に対する考察が綴られており, 読みやすい文体で書かれているので興味があれば読んでみることを勧める.
本エントリはそのような意味で, 特に面白みもなくただ単に高校数学 Ⅲ までの三角関数の内容を復習しているだけのものとなっているので, その点は悪しからず.
加法定理
この間で余弦定理を暗に認めたものとして利用する.
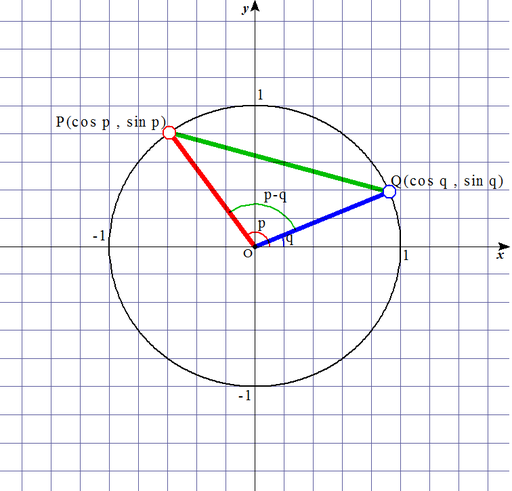
単位円上の二点 \(P\left(\cos p,\sin p\right),Q\left(\cos q,\sin q\right)\) がある.
上図のように, 原点 \(O\) に対し, \(O P\) と \(x\) 軸の成す角を \(p\),
\(O Q\) と \(x\) 軸の成す角を \(q\) とする. 線分 \(P Q\) の長さを座標成分で表すと,
\begin{eqnarray}
P Q^2&=&\left(\cos q-\cos p\right)^2+\left(\sin q-\sin p\right)^2\\\
&=&\cos^2 q-2\cos q\cos p+\cos^2 p+\sin^2 q-2\sin q\sin p+\sin^2 p\\\
&=&\left(\sin^2 p+\cos^2 p\right)+\left(\sin^2 q+\cos^2 q\right)-2\cos q\cos p-2\sin q\sin p\\\
&=&2-2\left(\sin p\sin q+\cos p\cos q\right)\label{eq:first}\tag{1}
\end{eqnarray}
また, 余弦定理より
\begin{eqnarray}
P Q^2&=&O P^2+O Q^2-2 O P\cdot O Q\cos\left(p-q\right)\\
&=&1^2+1^2-2\cdot 1\cdot 1\cdot \cos\left(p-q\right)\\
&=&2-2\cos\left(p-q\right)\label{eq:second}\tag{2}
\end{eqnarray}
\(\eqref{eq:first},\eqref{eq:second}\) より
\[2-2\cos\left(p-q\right)=2-2\left(\cos p\cos q+\sin p\sin q\right)\leftrightarrow \cos\left(p-q\right)=\cos p\cos q+\sin p\sin q\label{eq:third}\tag{3}\]
ここで, \(\eqref{eq:third}\) の \(q\) を \(q+\frac{\pi}{2}\) とすると, 三角関数の定義より
\[
\cos\left\{p-\left(q+\frac{\pi}{2}\right)\right\}=\cos p\cos\left(q+\frac{\pi}{2}\right)+\sin p\sin\left(q+\frac{\pi}{2}\right)\leftrightarrow\sin\left(p-q\right)=\sin p\cos q-\cos p\sin q
\]
\(q=-q\) とおくと \[\sin\left(p+q\right)=\sin p\cos q+\cos p\sin q\label{eq:fourth}\tag{4}\] \(\square\)
三角関数の導関数
まず \(f(x)=\sin x\) の導関数 \(f’(x)\) について, 導関数の定義より
\begin{eqnarray}
f'(x)&=&\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\\
&=&\lim_{h\to 0}\frac{\sin(x+h)-\sin x}{h}\\
&=&\lim_{h\to 0}\frac{\sin x\cos h+\cos x\sin h-\sin x}{h}\ \because{\rm 加法定理}\ \eqref{eq:fourth}\ {\rm より}\label{eq:sixth}\tag{5}\\
&=&\lim_{h\to 0}\frac{\sin x\left(\cos h-1\right)+\cos x\sin h}{h}\\
&=&\lim_{h\to 0}\left\{\frac{\sin x\left(\cos h-1\right)}{h}+\frac{\cos x\sin h}{h}\right\}\\
&=&\lim_{h\to 0}\left(\sin x\underbrace{\frac{\cos h - 1}{h}}_{A}+\cos x\frac{\sin h}{h}\right)\label{eq:fifth}\tag{6}
\end{eqnarray}
項 \(A\) について
\begin{eqnarray}
\frac{\cos h-1}{h}\cdot\frac{\cos h+1}{\cos h+1}&=&\frac{\cos^2h-1}{h\left(\cos h+1\right)}\\
&=&\frac{-\sin^2 h}{h\left(\cos h+1\right)}\ \because\sin^2+\cos^2=1\\
&=&\frac{-\sin h\cdot\sin h}{h\left(\cos h+1\right)}\cdot\frac{h}{h}\\
&=&-\frac{\sin h}{h}\cdot\frac{\sin h}{h}\cdot\frac{h}{\cos h+1}
\end{eqnarray}
ここで, \(\displaystyle\lim_{h\to 0}-\frac{\sin h}{h}\cdot\frac{\sin h}{h}\cdot\frac{h}{\cos h+1}=0\) だから,
\(\eqref{eq:fifth}\) より \[f’(x)=\sin x\cdot 0+\cos x\cdot 1=\cos x\label{eq:tenth}\tag{7}\]
次に \(f(x)=\cos x\) の導関数 \(f’(x)\) について, 導関数の定義より
\begin{eqnarray}
f'(x)&=&\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\\
&=&\lim_{h\to 0}\frac{\cos(x+h)-\cos x}{h}\\
&=&\lim_{h\to 0}\frac{\cos x\cos h-\sin x\sin h-\cos x}{h}\ \because{\rm 加法定理}\ \eqref{eq:third}\ {\rm より}\label{eq:ninth}\tag{8}\\
&=&\lim_{h\to 0}\frac{\cos x\left(\cos h-1\right)-\sin x\sin h}{h}\\
&=&\lim_{h\to 0}\left\{\frac{\cos x\left(\cos h-1\right)}{h}-\frac{\sin x\sin h}{h}\right\}\\
&=&\lim_{h\to 0}\left(\cos x\frac{\cos h - 1}{h}-\sin x\frac{\sin h}{h}\right)\\
&=&\cos x\cdot 0-\sin x\cdot 1\\
&=&-\sin x\label{eq:eleventh}\tag{9}
\end{eqnarray}
次に \(f(x)=\tan x\) の導関数 \(f’(x)\) について,
これは \(f’(x)=\left(\tan x\right)’=\left(\frac{\sin x}{\cos x}\right)’\) だから
\begin{eqnarray}
f'(x)&=&\left(\frac{\sin x}{\cos x}\right)'\\
&=&\frac{\left(\sin x\right)'\cos x-\sin x\left(\cos x\right)'}{\cos^2 x}\\
&=&\frac{\cos x\cos x-\sin x\left(-\sin x\right)}{\cos^2 x}\ \because\eqref{eq:tenth},\eqref{eq:eleventh}\ {\rm より}\\
&=&\frac{\cos^2 x+\sin^2 x}{\cos^2 x}\\
&=&\frac{1}{\cos^2 x}
\end{eqnarray}
最後に \(f(x)=\frac{1}{\tan x}\) の導関数 \(f’(x)\) について,
これは \(f’(x)=\frac{1}{\tan x}=\left(\frac{\cos x}{\sin x}\right)’\) だから
\begin{eqnarray}
f'(x)&=&\left(\frac{\cos x}{\sin x}\right)'\\
&=&\frac{\left(\cos x\right)'\sin x-\cos x\left(\sin x\right)'}{\sin^2 x}\\
&=&\frac{-\sin x\sin x-\cos x\cos x}{\sin^2 x}\ \because\eqref{eq:tenth},\eqref{eq:eleventh}\ {\rm より}\\
&=&-\frac{\sin^2x+\cos^2x}{\sin^2x}\\
&=&-\frac{1}{\sin^2x}
\end{eqnarray}
和積の公式を用いた方法
\(\eqref{eq:sixth},\eqref{eq:ninth}\) の部分では加法定理を用いたが, 加法定理より導出できる和積の公式を用いても同様にして導出できる.
\(\eqref{eq:fourth}\) より
\begin{eqnarray}
\sin\left(p+q\right)&=&\sin p\sin q+\cos p\sin q\label{eq:seventh}\tag{10}\\
\sin\left(p-q\right)&=&\sin p\sin q-\cos p\sin q\label{eq:eightth}\tag{11}
\end{eqnarray}
\(\eqref{eq:seventh}+\eqref{eq:eightth}\) より \[\sin\left(p+q\right)+\sin\left(p-q\right)=2\sin p\cos q\leftrightarrow \sin p\cos q=\frac{\sin\left(p+q\right)+\sin\left(p-q\right)}{2}\label{eq:thirteenth}\tag{12}\]
また, \(\eqref{eq:third}\) より
\begin{eqnarray}
\cos\left(p+q\right)&=&\cos p\cos q-\sin p\sin q\label{eq:fifteenth}\tag{13}\\
\cos\left(p-q\right)&=&\cos p\cos q+\sin p\sin q\label{eq:sixteenth}\tag{14}
\end{eqnarray}
\(\eqref{eq:fifteenth}-\eqref{eq:sixteenth}\) より
\[\cos\left(p+q\right)-\cos\left(p-q\right)=-2\sin p\sin q\leftrightarrow \sin p\sin q=-\frac{\cos\left(p+q\right)-\cos\left(p-q\right)}{2}\label{eq:seventeenth}\tag{15}\]
\(\eqref{eq:thirteenth},\eqref{eq:seventeenth}\) は積和の公式といわれる (あともう 1 つ積和の公式と言われるものがあるが, 今回は利用しないので省略).
ここで, \(\eqref{eq:thirteenth}\) に対し \(p=\frac{x-y}{2},q=\frac{x+y}{2}\) とすると,
\begin{eqnarray}
\sin\frac{x-y}{2}\cos\frac{x+y}{2}&=&\frac{\sin\left(\frac{x-y}{2}+\frac{x+y}{2}\right)+\sin\left(\frac{x-y}{2}-\frac{x+y}{2}\right)}{2}\\
&=&\frac{\sin x-\sin y}{2}
\end{eqnarray}
ゆえに
\[\sin x-\sin y=2\cos\frac{x+y}{2}\sin\frac{x-y}{2}\label{eq:twelvth}\tag{16}\]
また \(\eqref{eq:seventeenth}\) に対し \(p=\frac{x+y}{2},q=\frac{x-y}{2}\) とすると,
\begin{eqnarray}
\sin\frac{x+y}{2}\sin\frac{x-y}{2}&=&-\frac{\cos\left(\frac{x+y}{2}+\frac{x-y}{2}\right)-\cos\left(\frac{x+y}{2}-\frac{x-y}{2}\right)}{2}\\
&=&-\frac{\cos x-\cos y}{2}
\end{eqnarray}
ゆえに
\[\cos x-\cos y=-2\sin\frac{x+y}{2}\sin\frac{x-y}{2}\label{eq:fourteenth}\tag{17}\]
\(\eqref{eq:twelvth},\eqref{eq:fourteenth}\) が和積の公式である (あともう 2 つ和積の公式と言われるものがあるが, 今回は利用しないので省略).
\(\eqref{eq:twelvth}\) をつかって \(\displaystyle f’(x)=\lim_{h\to 0}\frac{\sin\left(x+h\right)-\sin x}{h}\) を変形すると,
\begin{eqnarray}
f'(x)&=&\lim_{h\to 0}\frac{\sin\left(x+h\right)-\sin x}{h}\\
&=&\lim_{h\to 0}\frac{2\cos\left(\frac{2x+h}{2}\right)\sin\frac{h}{2}}{h}\ \because\eqref{eq:twelvth}\\
&=&\lim_{h\to 0}\frac{\cos\left(\frac{2x+h}{2}\right)\sin\frac{h}{2}}{\frac{h}{2}}\\
&=&\cos\left(\frac{2x}{2}\right)\\
&=&\cos x
\end{eqnarray}
と \(\eqref{eq:tenth}\) と同様の結果が得られる.
また, \(\eqref{eq:fourteenth}\) をつかって \(\displaystyle f’(x)=\lim_{h\to 0}\frac{\cos\left(x+h\right)-\cos x}{h}\) を変形すると,
\begin{eqnarray}
f'(x)&=&\lim_{h\to 0}\frac{\cos\left(x+h\right)-\cos x}{h}\\
&=&\lim_{h\to 0}\frac{-2\sin\left(\frac{2x+h}{2}\right)\sin\frac{h}{2}}{h}\ \because\eqref{eq:fourteenth}\\
&=&\lim_{h\to 0}-\frac{\sin\left(\frac{2x+h}{2}\right)\sin\frac{h}{2}}{\frac{h}{2}}\\
&=&-\sin\left(\frac{2x}{2}\right)\\
&=&-\sin x
\end{eqnarray}
と \(\eqref{eq:eleventh}\) と同様の結果が得られる.
参考文献
- 『三角関数とは何か』2018 年 9 月 6 日アクセス.
- 高木貞治 (1983) 『解析概論』岩波書店